Bảng công thức lượng giác đầy đủ, chi tiết, dễ hiểu

19/04/2021
Tin tức

Công thức lượng giác rất phổ biến trong các kỳ thi trung học phổ thông, cũng như trong các kỳ thi đại học. Chính vì vậy học thuộc lòng công thức lượng giác là bài học bắt buộc cho các bạn muốn dự các kỳ thi này. Dưới đây là các công thức lượng giác mà phucngocan.com đã tổng hợp từ cơ bản đến nâng cao và cách học thuộc lòng nhanh nhất cho các bạn nhé.

1. Kiến thức cơ bản về lượng giác

Lượng giác là một nhánh của toán học, dùng để tìm hiểu về hình tam giác và sự liên hệ giữa các cạnh và góc của hình tam giác. Hàm số lượng giác diễn tả các mối liên kết và được áp dụng để nghiên cứu tam giác và những hiện tượng có chu kỳ, chẳng hạn như như sóng âm.

Đường tròn lượng giác là 1 đường tròn sẽ như hình bên dưới

Đường tròn lượng giác

Trong đó, trục Oy là trục sin, trục Ox là trục cos, trục tang là đường thẳng tiếp giáp với đường tròn và song song với trục Oy, trục cotang là đường thẳng tiếp giáp với đường tròn và song song với trục Ox.

Bán kính hình tròn là OM, có giá trị bằng 1, cách xác định sin α và cos α như sau:

Giá trị sin cos

Mối liên quan giữa tan α và cot α với sin α và cos α

Giá trị tan cot

2. Bảng công thức lượng giác và các cung liên quan đặc biệt đầy đủ nhất

2.1. Lượng giác cơ bản

Lượng giác cơ bản

2.2. Các cung có liên quan đặc biệt

Cung đối nhau:

Cung đối nhau

Cung bù nhau: x và π-x:

Cung bù nhau

Cung phụ nhau: x và π⁄2 – x:

Cung phụ nhau

Cung hơn kém nhau π : x và π + x:

Cung hơn kém nhau π

Cung hơn kém nhau π⁄2 : x và x + π⁄2

Cung hơn kém nhau π/2

2.3. Công thức cộng

Công thức cộng

2.4. Công thức nhân đôi

Công thức nhân đôi

2.5. Công thức hạ bậc

Công thức hạ bậc

2.6. Công thức tính sin x, cos x, tan x theo t=tan⁡ x/2

Công Thức Tính sin x, cos x, tan x theo t=tan⁡ x/2

2.7. Công thức nhân ba

Công thức nhân ba

2.8. Công thức biến đổi tổng thành tích

Công Thức Biến Đổi Tổng Thành Tích

2.9. Công thức biến đổi tích thành tổng

Công thức biến đổi tích thành tổng

3. Các công thức lượng giác nâng cao

3.1. Các công thức kết hợp với các hằng đẳng thức đại số

Các công thức kết hợp với các hằng đẳng thức đại số

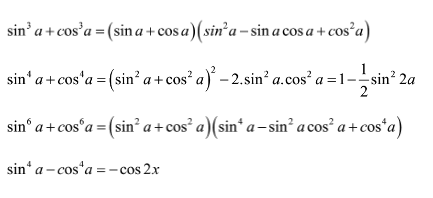
3.2. Công thức hạ bậc

Công thức hạ bậc nâng cao

3.3. Công thức liên quan đến tổng và hiệu các giá trị lượng giác

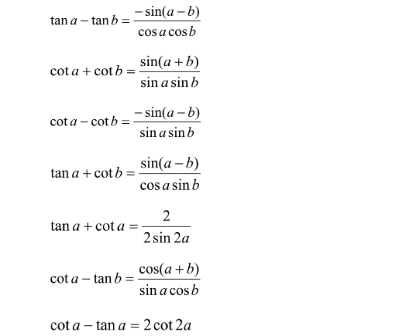
Công thức liên quan đến tổng và hiệu các giá trị lượng giác

Xem thêm:

4. Cách học thuộc công thức lượng giác nhanh nhất

4.1. Bài thơ về công thức cộng lượng giác

Cos + cos = 2 cos cos

Cos trừ cos = trừ 2 sin sin

Sin + sin = 2 sin cos

Sin trừ sin = 2 cos sin

Sin thì sin cos cos sin

Cos thì cos cos sin sin “coi chừng” (dấu trừ).

Tang tổng thì lấy tổng tang

Chia một trừ với tích tang

4.2. Cách học thuộc giá trị lượng giác cung đặc biệt

Cos đối, sin bù, phụ chéo, khác pi tan
Cosin của 2 góc đối bằng nhau; sin của 2 góc bù nhau thì bằng nhau; phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tan góc này = cot góc kia; tan của 2 góc hơn kém pi thì bằng nhau.

4.3. Cách học thuộc công thức lượng giác nhân ba

Nhân ba một góc bất kỳ

Sin thì ba bốn, cos thì bốn ba

Dấu trừ đặt giữa 2 ta, lập phương chỗ bốn

4.4. Công thức gấp đôi

Sin gấp đôi = 2 sin cos

Cos gấp đôi = bình cos trừ bình sin = trừ 1 + 2 lần bình cos = + 1 trừ 2 lần bình sin

Tang gấp đôi

Tang đôi ta lấy đôi tang (2 tang)

Chia 1 trừ lại bình tang, ra liền

4.5. Cách học thuộc công thức lượng giác biến đổi tổng thành tích nhanh nhất

Sin tổng lập tổng sin cô

Cô tổng lập hiệu đôi cô đôi chàng

Còn tan tử + đôi tan (hoặc là: tan tổng lập tổng 2 tan)

Một trừ tan tích mẫu mang thương sầu

Gặp hiệu ta chớ lo âu

Đổi trừ thành + ghi sâu vào lòng

4.6. Cách nhớ công thức lượng giác biến đổi tích thành tổng dễ nhất

Cos cos nửa cos-+, + cos-trừ
Sin sin nửa cos-trừ trừ cos-+
Sin cos nửa sin-+ + sin-trừ

Trên đây là các công thức lượng giác toán cơ bản và nâng cao mà phucngocan.com đã tổng hợp. Để có thể làm tốt các bài tập rút gọn biểu thức hay chứng minh biểu thức lượng giác các bạn cần phải học thuộc lòng các công thức lượng giác trên. Hy vọng các bạn học thuộc các công thức này thành công và đạt điểm tốt trong các bài kiểm tra lượng giác.

Xem thêm các bài viết sau: